JAUFFRES David
Maître de Conférence
Phelma/Grenoble-INP
1130 Rue de la Piscine, Batiment ECOMARCH
BP75, 38402 St Martin d'Heres cedex
04 76 82 64 26
Contact e-mail
Teaching
Numerical Methods (BIOMED 2A)
Simulation Projects (BIOMED 2A)
Material and process selection (SIM 3A)
Materials science modelling projects (SIM3A)
Materials science practical works (SIM 2A)
Research interest : Ceramics - Fracture and damage - Sintering - Discrete simulations - Multi-physics modeling - 3D characterization - Sintering-assisted additive manufacturing
My research activities are focused on the numerical and experimental study of the sintering and the mechanical behavior of ceramic materials, in particular the relation to their microstructure (porous or not). For this purpose, an original modeling based on the discrete elements method has been developed according to two approaches, one adapted to microstructures having a granular character (partially sintered powders) and the other one adapted to continuous media. Beside that, I also work on the modeling of functional properties of these materials, their processing by sintering-assisted additive manufacturing, the 3D characterization of their microstructures and their experimental mechanical characterization.
HDR thesis (in french): Céramiques aux échelles de la microstructure et de l'architecture : frittage, propriétés en service et rupture
HDR defense slides (in english)
One slide presentation of my research activities
Publication list : google scholar
Talks : figshare.com
PhD Students
2023 - ... E. Nouguier "Multi-material additive manufacturing by 3D extrusion printing and sintering: experimental and numerical studies"
2022 - ... A. Bigeard "Etude de l’évolution des propriétés mécaniques et de la consolidation d’un réfractaire tempéré en service"
2021 - ... S. Panisset "Optimization of high performance nano-architectured electrode/electrolyte bilayers
for reversible Solid Oxide Cells" (Coll. with M. Burriel / LMGP)
2019 - 2022 B. Paredes-Goyes "Discrete Element Modeling of constrained sintering" (Mathegram ITN)
2018 - 2021 G. Hamelin "Silica aerogel based thermal super-insulation panels: mechanical properties optimization"
2016 - 2020 N. Khamidy "Microstructure and durability of praseodymium-doped lanthanum nickelate for solid oxide cells"
2016 - 2019 K. Radi "Bioinspired materials : Optimization of the mechanical behavior using Discrete Element Method"
2015 - 2018 E. Guesnet - "Modélisation du comportement mécanique et thermique des silices nano-architecturées"
2013 - 2016 O. Celikbilek - "An experimental and numerical approach for tuning the cathode for high performance IT-SOFC"
Recently published work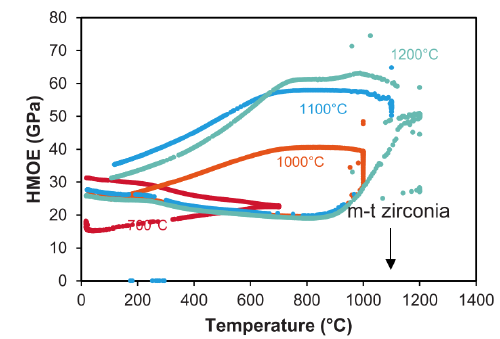
Effect of various thermal treatments on the elastic modulus (HMOE) of alumina-mullite-zirconia refractory. A. Bigeard et al., JECerS, in press (2023)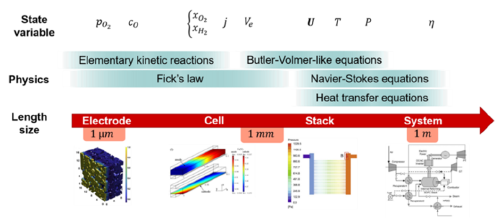
Modelling of SOCs from the electrode to the system scale. S. Panisset et al., Journal of Physics: Energy, 5, 022003 (2023)
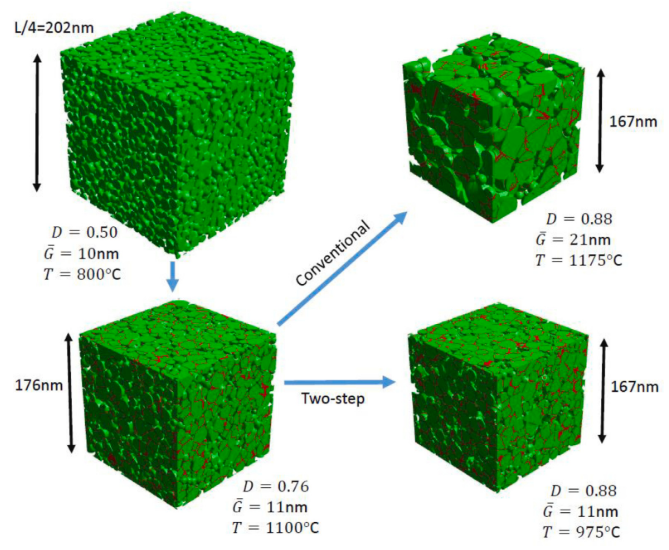
Discrete simulations of microstructure evolution during conventional and two step sintering. B. Paredes-Goyes et al., JECerS, 43, 501-09 (2023)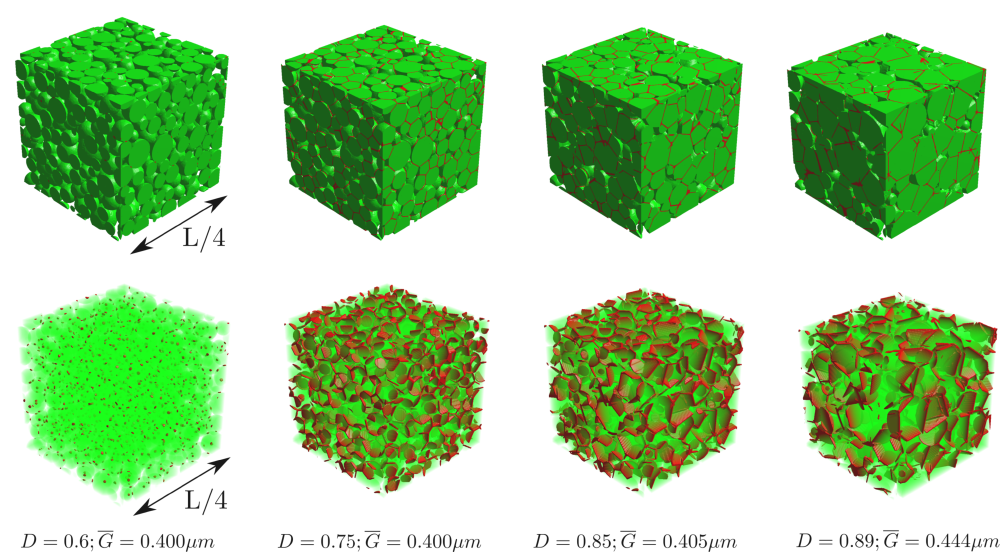
Evolution of the microstructure during a discrete element simulation of sintering with grain growth. B. Paredes-Goyes et al., Acta Materialia, 218 117182 (2021).
My research activities are focused on the numerical and experimental study of the sintering and the mechanical behavior of ceramic materials, in particular the relation to their microstructure (porous or not). For this purpose, an original modeling based on the discrete elements method has been developed according to two approaches, one adapted to microstructures having a granular character (partially sintered powders) and the other one adapted to continuous media. Beside that, I also work on the modeling of functional properties of these materials, their processing by sintering-assisted additive manufacturing, the 3D characterization of their microstructures and their experimental mechanical characterization.
HDR thesis (in french): Céramiques aux échelles de la microstructure et de l'architecture : frittage, propriétés en service et rupture
HDR defense slides (in english)
One slide presentation of my research activities
Publication list : google scholar
Talks : figshare.com
PhD Students
2023 - ... E. Nouguier "Multi-material additive manufacturing by 3D extrusion printing and sintering: experimental and numerical studies"
2022 - ... A. Bigeard "Etude de l’évolution des propriétés mécaniques et de la consolidation d’un réfractaire tempéré en service"
2021 - ... S. Panisset "Optimization of high performance nano-architectured electrode/electrolyte bilayers
for reversible Solid Oxide Cells" (Coll. with M. Burriel / LMGP)
2019 - 2022 B. Paredes-Goyes "Discrete Element Modeling of constrained sintering" (Mathegram ITN)
2018 - 2021 G. Hamelin "Silica aerogel based thermal super-insulation panels: mechanical properties optimization"
2016 - 2020 N. Khamidy "Microstructure and durability of praseodymium-doped lanthanum nickelate for solid oxide cells"
2016 - 2019 K. Radi "Bioinspired materials : Optimization of the mechanical behavior using Discrete Element Method"
2015 - 2018 E. Guesnet - "Modélisation du comportement mécanique et thermique des silices nano-architecturées"
2013 - 2016 O. Celikbilek - "An experimental and numerical approach for tuning the cathode for high performance IT-SOFC"
Recently published work
- Thermomechanical behavior of an alumina-mullite-zirconia refractory ceramic: sintering and thermally induced damage

Effect of various thermal treatments on the elastic modulus (HMOE) of alumina-mullite-zirconia refractory. A. Bigeard et al., JECerS, in press (2023)
- Modelling of solid oxide cell oxygen electrodes

Modelling of SOCs from the electrode to the system scale. S. Panisset et al., Journal of Physics: Energy, 5, 022003 (2023)
- Two-step sintering of alumina nano-powders: A discrete element study

Discrete simulations of microstructure evolution during conventional and two step sintering. B. Paredes-Goyes et al., JECerS, 43, 501-09 (2023)
- Grain growth in sintering: A discrete element model on large packings

Evolution of the microstructure during a discrete element simulation of sintering with grain growth. B. Paredes-Goyes et al., Acta Materialia, 218 117182 (2021).


